作者|kipply
翻译|杨婷、徐佳渝、贾川
本文具体论述了大型语言模型推理性能的几个基本原理,不含任何试验数据或简单的数学公式,旨在加深读者对相干原理的了解。此外,作者还提出了一种极其简略的推理时延模型,该模型与实证后果拟合度高,可更好地预测和解释Transformer模型的推理过程。
为了更好地浏览本文,读者需理解一些Transformer模型的相干先验常识,比方《图解Transformer》的大部分内容。另外,理解与本文相干的参数计数文章也能更好地帮忙读者了解本文内容。本文次要包含以下内容:
- kv 缓存 (kv cache) 解释了在推理过程中缓存自注意力向量所带来的性能优化成果,以及可能导致的衡量(tradeoff)以及容量老本问题。
- 容量(capacity)思考了kv缓存的存储老本以及模型权重的存储老本之间的分割,并解释了容量大小对模型性能的影响。
- 模型并行可帮忙咱们了解张量并行,以明确通信老本。
- 时延计算须要从其余概念中取得了解,并创立用于确定推理速度底线(floorline)的方程。
- 批大小(batch size)对性能的影响以及最优批大小为多少。
- 通过transformer blocks执行flops(每秒浮点运算次数)计数操作,能够辨认对flops速度有实质性奉献的操作。
- 两头内存老本涵盖了激活(即激活函数的输入后果)占用额定内存,以及一些实在基准测试中的内存带宽老本。
- 比照实在基准测试是指将计算出的内容与英伟达 FasterTransformer基准测试后果进行比照,并确定其中的差别。
(本文经受权后由OneFlow编译公布,译文转载请分割OneFlow取得受权。原文:https://kipp.ly/blog/transformer-inference-arithmetic/)
1
kv 缓存
采样时,Transformer模型会以给定的prompt/context作为初始输出进行推理(能够并行处理),随后逐个生成额定的token来持续欠缺生成的序列(体现了模型的自回归性质)。在采样过程中,Transformer会执行自注意力操作,为此须要给以后序列中的每个我的项目(无论是prompt/context还是生成的token)提取键值(kv)向量。这些向量存储在一个矩阵中,通常被称为kv缓存或者past缓存(开源GPT-2的实现称其为past缓存)。past缓存通常示意为:[batch, 2, num_heads, seq_len, features]。
kv缓存是为了防止每次采样token时从新计算键值向量。利用事后计算好的k值和v值,能够节俭大量计算工夫,只管这会占用肯定的存储空间。每个token所存储的字节数为:
第一个因子2示意k和v这两个向量。在每一层中咱们都要存储这些k,v向量,每个值都为一个矩阵。而后再乘以2,以计算每个向量所需的字节数(在本文中,咱们假如采纳16位格局)。
咱们乘以token嵌入(token embeddings)失去的权重为,其中每个token嵌入为
。这样,咱们就能够算出所有层的k和v需进行的浮点运算次数为:
将乘以须要进行次浮点运算。另一个2示意咱们须要反复两次这样的操作,一次用于计算k和一次用于计算v,而后再反复所有层数。
矩阵乘法(matmul)中的浮点运算次数为多少?
矩阵-向量(matrix-vector)乘法的计算公式是 ,其中 ,。对于矩阵-矩阵(matrix-matrix)乘法,计算公式是 ,其中,。因子非常重要,因为它反映了矩阵乘法中由乘法和加法组成的组合形式,即“乘法(1)-加法(2) 操作组合”。更多内容见讲义(lecture notes)。
这意味着对于一个520亿参数的模型来说 (以Anthropic中的模型为例,,
),其浮点运算次数为:
假如有一个A100 GPU,其每秒可执行的浮点运算次数为
,其内存带宽可达字节/秒。以下数字仅波及kv权重及计算的数值:
Flops vs 内存有界性(Boundedness)
英伟达应用了数学带宽这个术语,我感觉这个术语真的很可恶。从技术上讲,这种形容存在于每个内核中,但能够形象为操作组。
Flops vs 内存有界性是Transformer推理和深度学习优化的常见问题。为了实现所需计算,通常须要加载权重,加载过程会占用内存带宽。假如通过加载权重曾经失去了很好的优化,那么咱们能够在加载权重的同时开始计算。
在这种状况下,flop bound意味着一段时间内存中没有任何数据传输;memory bound则意味着没有进行任何计算操作。
英伟达应用数学带宽(math bandwidth)来形容该状况,我感觉相当有意思。从技术上讲,这种划分通常是指每个内核(kernel)中的计算量受限,但也能够指这些操作组的计算量受限,将每一组视为形象意义上的单元。
当初模型架构不再重要了——在给定硬件规格的状况下,咱们失去了一个显著的比率208。这意味着,咱们计算一个token的kv所需的工夫,与解决208个token的工夫雷同。若低于该值,会呈现内存带宽限度,若高于该值,会呈现flops限度。如果咱们应用残余的权重来实现残缺的前向传递(即运行残余的transformer),那么后果依然是208(分子和分母各乘以6)。这一点咱们会在前面的章节具体介绍。
下图的交点是208,不过实际上内存线(memory line)会有一些歪斜,这是因为两头计算(intermediate calculation)存在内存老本(上一节探讨过)。
对于领有520亿参数的模型来说,一次残缺的前向传递须要毫秒,这是解决208个token所需的工夫(实际上咱们会应用四个GPU进行并行处理,因而理论须要的工夫约为17毫秒,后续章节将做具体介绍)。如果语言环境存在416个token(即双倍token),那么解决工夫将翻倍,而解决312个token所需的工夫是解决208个token的1.5倍。
计算kv缓存的token时,一个token所需的计算成本为模型中传递该token计算成本的1/6。总的来说,这些前向传递(获取logits、嵌入和训练时咱们深有体会)十分便宜,因为能够进行并行计算。相比之下,采样的老本要高得多,因为它须要强制读取每个token的所有权重,进行自回归预测。
但这并不意味着工夫节俭了1/6!假如呈现了flops bound,在每个采样步骤中,咱们能够少进行次浮点运算,而解码步骤(step)须要进行次浮点运算。
因而,在每个步骤中,咱们节俭的每秒浮点运算次数是序列中每个token每秒浮点运算次数的1/6(很大!),而且该数值会随着采样token数量的减少而减少。在没有kv缓存的状况下,随着token数量的减少,采样的工夫复杂度(time complexity)将以平方级减少。
思考到存储缓存相干的开销和衡量(tradeoffs),以上说法并不全面。如果咱们进行小批量设置,可能会呈现内存带宽受限,而非flops bound。在这种状况下,咱们可能不会应用过来的缓存,而是偏向于从新计算,这会耗费flops(因为咱们曾经领取了采样的内存老本)。
2
容量
咱们对于GPU中存储的kv缓存和权重有了肯定意识,并且理解到GPU容量的确对Transformer模型的推理性能有着重要影响,也就有了充沛的理由对其进行评估。
一般来说,Nvidia A100 GPU是用于推理的最佳GPU,其容量规范为40GB。尽管有一些GPU的容量高达80GB,并且具备更高的内存带宽(为 2e12 而非 1.5e12),但它们尚未被任何大型云服务提供商采纳,因而,于我而言它们不足理论价值。
将给定的参数计数(parameter count)乘以2,咱们就能够获取相应字节数,进而算出领有520亿参数的模型的权重大小。
不过这显然不能在一个GPU上实现,咱们至多须要三个GPU能力加载所有权重(稍后将探讨如何进行分区(sharding))。但这样就只剩下可用kv缓存了,这足够吗?让咱们回到kv缓存内存中每个token的方程式,再次应用520亿参数大小的模型运行。
应用这种GPU设置,咱们能够将个token存储在kv缓存中。或者咱们能够将batch size设置为4,其中每个申请最多蕴含2048个token(token越少所需batch size越大)。
难办的是,咱们想要做更高的batch size,但却受到容量限度。batch size越大,GPU解决雷同申请所需的工夫就越短,就能更无效地利用GPU资源。然而,batch size小,内存又会受到限制。在这种状况下,应该放弃应用kv缓存,抉择领取flops老本。
同时应用四个GPU,就能解决个token。要想batch size更大,解决更多的数据,咱们必定会抉择四个GPU。若只用一个GPU,会升高2/3的效率,这显然不是理智的做法。这不仅是batch size的问题,如果有大量的数据须要解决,那应该应用多个模型实例。咱们的指标应该是,尽可能让每个实例都能够通过更大的batch size解决,因为无奈防止领取存储权重的老本。
两头计算步骤会占用一些额定空间,但这些空间能够忽略不计。
3
模型并行
这方面已有许多相干介绍,所以我就不再具体介绍模型并行(model parallelism)及其实现细节了,仅提供一些有用信息,以帮忙读者做性能决策并计算通信老本。
模型并行的最终后果:通过内存和flops传输的所有权重老本都被摊派到应用的加速器数量上。
咱们将采纳张量并行(一种模型并行),将模型的两头进行划分。每个加速器将应用其权重分片(shards)尽可能多地执行操作,并在须要同步时进行通信。相比之下,流水并行(pipeline parallel)更为简略,其中每个GPU将保留模型的一部分层。尽管这种办法确实均衡了权重加载老本,但存在显著缺点:只有一个GPU运行,其余的都被闲置!
在训练过程中,你能够采纳流水并行(第一批数据移向下一个GPU时,新一批数据从新于第一个GPU开始),以便无效利用各个GPU。尽管解决多个样本申请时该办法非常有用,但在解决单个样本申请时,这种办法就不太见效了。此外,无论flops是否受限,流水线并行都无奈充分利用内存带宽。简而言之,流水并行实用于通信,而模型并行实用于计算。流水并行会在每个加速器之间进行次通信,而模型并行会在每个层内进行次通信,其中是加速器的数量。
A100 GPU的通信带宽为300GB/s,而文档将其标记为600GB/s,这是因为NVIDIA 在每颗芯片上叠加了300GB/s的带宽,同时向外输入300GB/s的带宽,而没有应用双向数值(对于计算,这种办法更为直观)。
首先,咱们在图中黄色区域将token嵌入(token embedding)插入到模型底部。紫色盒子形容了权重在加速器上的分配情况,此处咱们应用的是一个十分小的框架,以便可能按比例绘制所有内容。
广泛的做法是,咱们能够将两个矩阵!和进行划分,并计算shards的乘积,但这并不能实现的矩阵乘法(matmul)。换言之,如果咱们只是简略地将shards的乘积连贯在一起,那么失去的矩阵就会太大,无奈存储或进行计算。相同,如果咱们想要进行传输,能够计算出shard sum,并将shard sum进行通信,而后进行连贯到输入。
注意力机制通常波及多头(head),因而采取并行计算十分直观。简直不须要通信就能走完大部分注意力层,因为注意力头(attention head)是连贯在一起的,须要乘以权重进行计算。在乘当前,咱们须要将后果乘以shard的,以失去。
而后,每个加速器会将本身的shard传递给其余加速器,其余加速器也会将其shard返回,其通信老本为。每个加速器平等调配相加的shard,以取得输入投影(output projection,译者注:输入层的输入被称为输入投影,它是一种将神经网络的输入转换为特定格局的过程。)而后,他们会反复上次进行的通信,各个主机进行连贯(近似霎时就能实现)。
其本质与MLP(Multi-Layer Perceptron)层相似!就像咱们使用权重将多头注意力(multi-headed attention)的后果投射回长度为的向量一样。同样,咱们也应用和将向量维度扩充4倍,并将其从新投射回原始值大小。因而,在MLP的末端实现了两次同样的通信。
咱们最终的通信量为字节。GPU将对整个kv缓存进行划分,并将其调配到各个头部。
4
时延计算
咱们曾经较全面地探讨了容量(capacity)、模型并行中的通信,以及个别的计算步骤。接下来咱们将其构建到预计时延的方程中!
时延计算大多与flops和内存有界性相干。如果每个参数须要进行的乘法运算很少,那么咱们可能会受到内存带宽的限度。浮点运算量减少取决于批处理大小和参数数量,而内存只受参数数量的影响。
通信方面,要害不是有界性问题,而是减少时延项和吞吐量项(即300GB/s)。因为时延方面的数据不通明,最理想化的预计也是每条音讯发送大概须要8微秒。该数据源于Citadel的一篇论文,但该论文针对的是V100 NVLink。
受计算因素的影响,计算单个token解码步骤的时延工夫须要两个公式:一个用于内存带宽bound(小batch),另一个用于 flops bound(大batch)。解决大batch数据时,咱们通常会疏忽通信的时延因素。
针对小batch(当batch size=1时,能够疏忽batch因素)的方程如下(其中N为加速器数量,P为参数数量,b示意字节单位):
因为咱们须要通过内存传递所有参数,且每个参数都是2字节,所以这里是2*P。是加速器内存带宽,老本在加速器之间摊派。每层有个通信申请,每个申请的时延较小,通常能够疏忽。通信还有吞吐老本,但也能够疏忽。
有时读取kv缓存的工夫也会对计算产生重要影响。不过,因为该因素取决于前后token的数量,而数量在同一批次内会有所变动,咱们要采样的总token数量也有所不同,因而临时将其排除在计算之外。这个工夫会被计算为内存带宽工夫。另一个缺失的内存带宽工夫是读取unembeddings,以计算每个采样步骤的logits,即。
如前所述,内存实际上并非放弃不变,每个批次会应用一些额定的内存来存储两头激活值。咱们之所以不计算这些额定内存,是因为其数量深受软件堆栈、编译器优化等因素的影响,很难准确计算。
针对大batch(batch size=512)的方程如下(其中 B 是批量大小):
其中,示意加速器的浮点运算能力,示意处理单元之间的通信带宽。公式中做了2*P次浮点运算,这从对所有参数进行矩阵相乘也可看出。如前所述,因为,所以矩阵向量乘法是2mn。
在模型并行局部,每个层须要进行四次(N-1个因子,四舍五入为至N)大小向量的通信。思考到时延能够忽略不计,这里应用吞吐量来计算通信工夫。将须要传输的总数据量除以通信带宽,能够失去通信所需工夫。
接下来,在16个GPU上应用2600亿参数的Gopher模型来进行推理。应用小batch推理时,生成一个token须要22毫秒的工夫。通过大batch公式计算出来的通信吞吐量老本约为35微秒,因而能够释怀地升高该老本。
对于512的大batch,生成每个token所需的工夫为53毫秒(即在62毫秒内生成512个token)。通信的时延老本也为3毫秒(因为音讯能够一起筹备,因而延时延不会随着batch的减少而减少),这对于缩小时延来说有肯定的意义,但如果假如通信和计算是并行的,那么这也能够承受。
在假设并行处理的状况下,咱们会抉择计算和通信中较大的值。因而,咱们心愿防止通信工夫大于计算工夫(这是避免随着芯片数量的减少趋近于零时延的机制,最终通信工夫将占用越来越多的工夫)。但并不能保障所有零碎都可能完满地并行处理。
这些数值显著比“沙箱环境”中取得的值要低得多(译者注:“沙箱环境”即一个独立于操作系统和其余程序运行的平安环境。在这个环境中,程序只能应用被受权的资源,无奈对系统或其余程序产生影响),因为它假如了最佳的硬件应用,没有思考softmax,假如没有通信时延,并疏忽了许多其余较小的因素。尽管如此,这些数学推理仍有助于思考如何优化性能以及将来优化所带来的变动。
5
Batch sizes
(Batch sizes)批大小是性能的一个重要因素,尤其是对特定用处性能的了解。
咱们在后面局部进行了两个计算,用于确定何时是内存带宽bound,何时是flops bound。为了确定主导因素,咱们能够对这些数值进行比照。
咱们正在解决与kv缓存局部雷同的比率。内存带宽bound的最小batch size为。该比率十分有用!在足够负载的状况下,咱们更偏向于flops bound,因为这样计算效率更高。然而,如果是flops bound,增大batch size并不会进步计算速度。
很容易计算出容量中的支流何时从kv缓存转变为权重,但这之间并没有显著的二进制分界点(当kv缓存开始占用更多内存时并不会有特地的变动)。此外,也没有特地重要的通信因素。随着batch size减少,吞吐量开始超过时延,所以咱们不再思考时延因素。正如之前察看到的,时延变得不重要的工夫绝对较晚(例如,52B通信老本上的512批大小仍有11%的时延)。
将其简化一下,即通信须要在四个不同的步骤中进行,这意味着咱们不仅心愿计算工夫比通信工夫长,而且在每个步骤中都是如此(如果咱们能够同时进行计算和通信)。为了达到这个指标,咱们应用一个更奇异的比率,即每个字节的通信量须要多少次浮点运算。下图是一个很好的计算表,后续内容也将会用到。
A100芯片每字节通信的浮点运算次数为(312e12/300e9)=1040次。咱们心愿最初一行的值大于硬件每字节的浮点运算次数,以放弃flops bound(假如没有memory bound)。对于任何embedding维度超过1024(每个芯片)的模型,绝对比拟平安!但对于512维度的模型而言,状况就有些辣手。 API负载较低时,会呈现较小的batch sizes,这时会思考放弃kv缓存等决策。
当API负载较高时,为了优化每个申请的时延,会抉择提供最低batch size,以达到flop bound,即便仍有容量残余。在AlphaCode等大规模推断工作中,咱们通常会尽可能多地插入芯片,而后利用这些容量执行最大的batch操作。尽管我常常应用“可能”一词,但这些状况都是相对存在的。
6
Flops计算
之前:
从所有参数的matmul操作来看,咱们的flops运算为2*P次。
这是很正当的推理,咱们还能够查看transformer步骤来合成推理,以核查是否能得出2P这个论断。
以下是对token和layer的计算。精确来说,应该表述为,其中i最大为。为了计算时延,我简化了,以蕴含所有heads。
qkv计算
将乘以
>Flop次数:
>计算z
>公式为: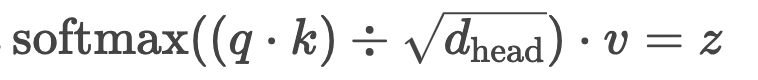>这里不须要矩阵乘,flops为的某个因子。
乘以输入投影矩阵(projection matrix)
将乘以
>Flop次数:
>前馈
咱们有用于两个线性变换的MLP权重和(两头有一个小的ReLU)。
Flop次数:
>其余
>通常每次attention后都会运行layernorm,其中权重为长度向量。
>这里还有另一个线性层,而后是位于顶部的softmax,softmax就是咱们的输入(token)嵌入(embedding)、解嵌(unembedding )、反嵌(de-embedding)或嵌入
( embedding)。
>原始transformer有余弦相对地位编码(cosine absolute positional encoding scheme),它是token嵌入的加法操作。
将所有flops相加!
在8192模型中,flops大概为100B;
103079215104除以2约等于515亿。咱们失去的后果为515亿,比520亿略少一些,这是因为token(un)embeddings的参数靠近了10亿,相比,更适宜用来计算时延,但这两者的差别不到2%。
该如何计算Z和其余步骤呢?这些都是向量到向量(甚至向量到标量)的运算,所以它们都是围绕因子建造起来的,而不是因子。即便每一层(layer)要运行100次这样的操作,最终也会有一亿次flops, 占已计算flops的0.1%。
7
两头内存老本
Data Movement Is All You Need(https://arxiv.org/pdf/2007.00072.pdf,次要内容是优化transformers的低层级数据挪动,与本文内容不太相干)一文提出了一个很好的分类操作方法。首先,在大矩阵(包含线性层)当中,张量缩并(tensor contractions)是最重要的,统计归一化(包含softmax和layernorm)次之,最初是逐元素操作,比方偏置( biases)、dropouts和激活(activations)等。
那么咱们该如何计算矩阵、layernorms等的时延呢?咱们硬件上报告的flops是专门针对乘加运算的,因而即便咱们能够计算flops,其后果也不对。侥幸的是,这只是为了占用内存来进行softmax读/写,因为这有利于带宽和flops比率。这是已知的时延因素!
在这里我将抛开第一性准则,探讨 Data Movement Is All You Need一文中的表格A.1。咱们发现softmax的时延工夫略长于qkv的计算工夫(softmax时延工夫是qkv操作工夫的三倍)。这有点令人担忧,可能会影响整个神经网络的性能。
出于同样的起因,softmax会受到内存限度,所以qk、ReLU和dropout的乘法(multiplication)操作也相当低廉。
GPU内核交融(Fusion)
GPU 以“内核”为单位执行操作。内核交融意味着2个内核能够交融为一个,这样咱们就能够在内存中反复利用负载,缩小冗余负载和存储。例如,一个乘加(multiply-add)是一个内核。然而如果一个乘加有两个内核,一个内核负责加载+加法+存储,另一个内核负责加载+乘法+存储。内核交融当前,咱们能够运行加载+加法+乘法+存储,以简化步骤。
通过计算所需的读写次数,咱们发现这里的softmax没有完满交融。实践上它能够是一次读取和一次写入(规范次数为四次)。qk是两次读取和一次写入(两次读取可能能够保留)。三比一的比率示意softmax执行的内存传递量多于最佳值。我这样说是因为,这表明了计算的软件依赖水平,并且须要通过试验来验证,因为从实践上来说老本可能为0。
值得注意的是,随着模型大小的减少,操作所破费的工夫百分比会迅速升高,因为每层内存将以减少,flops将以 减少。本文为336M参数模型,。
我将“Ours”列中内存限度的所有值的时延相加(包含 element-wise操作)。结果显示,两头步骤占用了43%的工夫。能够看到,这些操作在大小为520亿(是这个模型的八倍)的模型中没有那么重要。
这些memory bound两头操作的持续时间将缩短8倍,因为这些操作是长度的向量。然而,flops次数将减少64倍,这意味着flop工夫会缩短64倍。
因而,若不思考时延,应用 Data Movement Is All You Need中的优化办法,520亿参数模型的推理时延大概会是两头计算的 5%。
8
理论基准比照
我在语言建模公司工作,咱们公司有本人的基础设施和基准,但IP是公司面临的一大难题。可悲的是不足可用于模型并行推理的公共基准。目前我只晓得Nvidia的FasterTransformer和Microsoft的Deepspeed,可能其余我不理解的论文也提出了一些基准。无论如何,咱们能够依据实在基准来验证计算!
因为我只想用2个GPU,所以应用了FasterTransformer来运行了一个130亿参数的模型。该模型执行一连串内核交融,并提供张量并行性能。模型有40层,每层有40个头,每个头的维度为128,总维度大小为5120。这里是配置文件截图,这些截图显示了许多乏味的细节,可能值得独自撰写一篇文章。
首先是输入的512个上下文长度(context length)、batch size为1和10个token。对于2个GPU上的一个小batch的token,咱们预计为8.4毫秒,大概1毫秒的通信,那么一个GPU则是16.8毫秒,0毫秒的通信。(2x40x12x5120^2/1.5e12)
在这里我应该将内存宽带(mem bandwidth)设置为1.555,而不是1.5。
实测结果表明,1个GPU应该是22.0ms,这意味着,咱们的猜想的准确率为76%。能够确定,其中一部分工夫花在了两头激活操作上,从实践上来说,咱们能够取得100%的内存带宽,但实际上并没有。
对于这些维度,测试表明咱们能够取得高达90%的内存带宽利用率(咱们将矩阵乘法的预期老本与单个矩阵乘法内核的持续时间进行比拟,因为加载的张量不同,带宽利用率会有所变动)。思考到这一点,咱们预计须要18.5毫秒。加上两头激活操作的老本后(咱们能够从测试后果中取得),须要额定的2.2毫秒,总共须要20.7毫秒!
为了解释剩下的1.4毫秒,咱们思考到了一些其余的亚毫秒级操作,比方token嵌入、top-(k|p)操作、少于90%的带宽利用率(不想计算平均值,间接取了我能找到的最高带宽利用率),或者是内核启动工夫。
试验结果显示,应用2个GPU时,总工夫为13.5毫秒。相比一个GPU,这次咱们只占了内存宽带的76%,离指标还有很大的差距。为了解决这个问题,咱们从新查看了配置文件,发现内存带宽略微差了一些,因为张量较小获取的带宽也比拟少。
通过计算,宽带没有达到90%,只有87%,总工夫为9.5毫秒,两头的激活工夫须要大概2毫秒,这使得总工夫为11.7毫秒。残余的1.5毫秒须要找出通信问题。然而这个问题很容易解决,因为咱们之前计算的1毫秒通信工夫没有被并行化。依据配置文件的数据,每个层的通信工夫为40-50微秒,总共约为1.7毫秒,这就是很好的证实。
上述两种操作的两头激活计数都比应有的要高一些,因为配置文件提供的时延始终略高于原始基准测试运行。基准测试运行的输入为180.86ms(上下文工夫:45.45ms)和 283.60ms(上下文工夫:63.17ms)。
在前向传递过程中,模型须要将所有token发送到每个GPU上,而后每个GPU都会对其进行本人的注意力头计算并存储kv。因为这个过程须要发送大量的数据并进行并行计算,因而预计前向传递须要的工夫会比解码步骤长num_tokens/flops_to_bw_ratio倍。
更新的内存带宽为:312e12/(1.5e12x0.9)=231。在1个GPU的设置中,22ms是咱们预期的解码步骤,咱们能够失去22(512/231)= 48,并不是63。在2个GPU设置中,咱们通过计算失去了更加蹩脚的后果:13.5(512/231)=30ms。
单个GPU只缺失了局部kv贮存工夫。查看配置文件,咱们发现kv贮存工夫每层为18微秒,总共为0.7毫秒。Memsets占了0.2毫秒。咱们预计其中一个MLP乘法的flop工夫(flop bound)为512x4x5120^2×2/312e12 = 344微秒。实际上,最低浮点运算工夫应该是476微秒,也就是说,咱们失去了预期flops的72%。
对于attention中的投影(projection),咱们冀望是512×5120^2×2/312e12 =86微秒。然而在配置文件中,咱们发现最低是159微秒。请参阅本文的图14,其中512x4000x4000的最终后果低于150TFLOPs/s。
9、练习
1.在给定batch size、上下文长度和next_n的状况下,咱们该如何计算kv缓存节约的宽带?
2.kv缓存会减少内存工夫开销吗?
3.咱们是否能够在前向传递时抉择memory bound,在采样步骤中抉择flops bound?
4.在GPU超过容量所需的状况下,咱们应该进行怎么的衡量和计算?例如,一个520亿参数大小的模型(领有8或16个GPU)。
5.如果咱们有计算预测一个token工夫的公式。咱们应该如何计算执行整个样本的工夫呢?是否应该先在上下文上进行前向传递,再预测所有的申请token?
6.在容量局部,我曾提到两头计算的内存能够忽略不计。那么这些内存到底有多小呢?
7.在batch size局部,咱们探讨了每字节通信的token数。如果咱们的嵌入维度为512,咱们须要做怎么的衡量?
8.假如GPU都连贯到了同一主机,但能够像训练那样在主机之间进行GPU通信。AWS 有400GB/s。这种状况该怎么办呢?
9.在模型并行局部,咱们能够理论沟通所有分片(shards),而后让每个加速器执行所有增加(不只是其中一部分增加)。这部分会对时延产生怎么的影响呢?
10.在batch size为256的4xGPUs上计算520亿的大批量速度。计算约为21毫秒,通信约为4毫秒。
11.从最初一层中取出向量,将其乘以未嵌入矩阵,存储logits,而后进行top-k或top-p采样(须要排序)。对于一个蕴含520亿参数的模型,这个过程须要多长时间,咱们能够在这里并行化什么操作?
12.如何进行分片token嵌入?在输出token嵌入和未嵌入token之间,是否须要以不同的形式划分分片和应用层归一化(Layernorms),这会引起额定的通信开销吗?
欢送 Star、试用 OneFlow 最新版本:https://github.com/Oneflow-Inc/oneflow/
发表回复