分治法之棋盘笼罩复牌问题，c++ 实现

问题形容

一个棋盘，其中有一个非凡点，用 L 的骨牌去笼罩，骨牌不能重叠，如何做到全副笼罩，如图：

![在这里插入图片形容](https://img-blog.csdnimg.cn/3ba0eedd2e5944c1bbd6947513fed6f9.png)

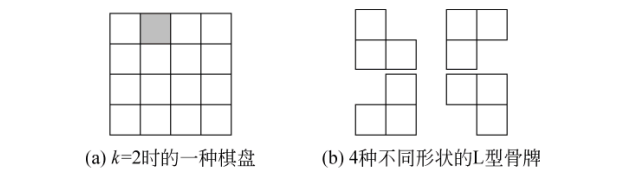
实现

1. 采纳分治法
2. 将一个棋盘划分为 4 个棋盘，有一个棋盘存在非凡点，其余三个棋盘没有非凡点
3. 将没有非凡点的棋盘连贯，用 L 型骨牌连贯三个棋盘，使每个棋盘变成有一个非凡点的子棋盘
4. 反复操作，直到大小为 1，算法完结

// 将一个棋盘划分为 4 个棋盘，则有三个棋盘是没有非凡点的，将这三个棋盘用一个 L 型骨牌连贯，将会失去一个规模小的子棋盘 
// # 假如非凡点的下标为 dr，dc，棋盘左上角坐标为 tr，tc，大小为 s 
// # 初始化，dr = 1，dc = 1；tr = 0；tc = 0；s = 8；// # 棋盘用 board[size][size] 二维数组示意，size = 2^k 
#include<iostream>
using namespace std;
const int n = 8;
int t = 1;
int board[n][n] = {0};
void chessBoard(int tr, int tc, int dr, int dc, int size) {if (size == 1) return;
    int t1 = ++t; // 牌号 +1
    int s = size / 2; // 划分棋盘为 4 块 
    // 别离针对非凡点的地位对棋盘进行递归 
    // 非凡点在左上角，tr+ s 示意左上角棋盘的范畴
    // 1. 左上角棋盘解决 
    if (dr < tr + s && dc < tc + s) {chessBoard(tr, tc, dr, dc, s); // 间接递归 
    } else {board[tr+s-1][tc+s-1] = t1; // 非凡点 
        chessBoard(tr, tc, tr+s-1, tc+s-1, s); // 左上角的棋盘非凡标记放在右下角 
    } 
    // 2. 右上角棋盘解决
    if (dr < tr + s && dc >= tc + s) {chessBoard(tr, tc+s, dr, dc, s); // 间接递归 
    } else {board[tr+s-1][tc+s] = t1; // 非凡点 
        chessBoard(tr, tc+s, tr+s-1, tc+s, s); // 右上角的棋盘非凡标记放在左下角 
    } 
    // 3. 左下角棋盘解决 
    if (dr >= tr + s && dc < tc + s) {chessBoard(tr+s, tc, dr, dc, s); // 间接递归 
    } else {board[tr+s][tc+s-1] = t1; // 非凡点 
        chessBoard(tr+s, tc, tr+s, tc+s-1, s); // 左下角的棋盘非凡标记放在右上角 
    } 
    // 4. 左上角棋盘解决 
    if (dr >= tr + s && dc >= tc + s) {chessBoard(tr+s, tc+s, dr, dc, s); // 间接递归 
    } else {board[tr+s][tc+s] = t1; // 非凡点 
        chessBoard(tr+s, tc+s, tr+s, tc+s, s); // 左上角的棋盘非凡标记放在右下角 
    } 
}

int main() {board[1][1] = t; 
    chessBoard(0, 0, 1, 1, n);
    for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {cout<< board[i][j] << "\t";
        }
        cout<<endl;
    }
    return 0;
}

如图，数字代表笼罩程序