背景
始终从事金融相干我的项目,所以对 BigDecimal 再相熟不过了,也曾看到很多同学因为不晓得、不理解或使用不当导致资损事件产生。
所以,如果你从事金融相干我的项目,或者你的我的项目中波及到金额的计算,那么你肯定要花工夫看看这篇文章,全面学习一下 BigDecimal。
BigDecimal 概述
Java 在 java.math 包中提供的 API 类 BigDecimal,用来对超过 16 位无效位的数进行准确的运算。双精度浮点型变量 double 能够解决 16 位无效数,但在理论利用中,可能须要对更大或者更小的数进行运算和解决。
个别状况下,对于不须要精确计算精度的数字,能够间接应用 Float 和 Double 解决,然而 Double.valueOf(String) 和 Float.valueOf(String) 会失落精度。所以如果须要准确计算的后果,则必须应用 BigDecimal 类来操作。
BigDecimal 对象提供了传统的 +、-、*、/ 等算术运算符对应的办法,通过这些办法进行相应的操作。BigDecimal 都是不可变的(immutable)的,在进行每一次四则运算时,都会产生一个新的对象,所以在做加减乘除运算时要记得要保留操作后的值。
BigDecimal 的 4 个坑
在应用 BigDecimal 时,有 4 种应用场景下的坑,你肯定要理解一下,如果使用不当,必然很惨。把握这些案例,当他人写出有坑的代码,你也可能一眼辨认进去,大牛就是这么练成的。
第一:浮点类型的坑
在学习理解 BigDecimal 的坑之前,先来说一个陈词滥调的问题:如果应用 Float、Double 等浮点类型进行计算时,有可能失去的是一个近似值,而不是准确的值。
比方上面的代码:
@Test
public void test0(){
float a = 1;
float b = 0.9f;
System.out.println(a - b);
}后果是多少?0.1吗?不是,执行下面代码执行的后果是 0.100000024。之所以产生这样的后果,是因为 0.1 的二进制示意是有限循环的。因为计算机的资源是无限的,所以是没方法用二进制准确的示意 0.1,只能用「近似值」来示意,就是在无限的精度状况下,最大化靠近 0.1 的二进制数,于是就会造成精度缺失的状况。
对于上述的景象大家都晓得,不再具体开展。同时,还会得出结论在迷信计数法时可思考应用浮点类型,但如果是波及到金额计算要应用 BigDecimal 来计算。
那么,BigDecimal 就肯定能防止上述的浮点问题吗?来看上面的示例:
@Test
public void test1(){BigDecimal a = new BigDecimal(0.01);
BigDecimal b = BigDecimal.valueOf(0.01);
System.out.println("a =" + a);
System.out.println("b =" + b);
}上述单元测试中的代码,a 和 b 后果别离是什么?
a = 0.01000000000000000020816681711721685132943093776702880859375
b = 0.01下面的实例阐明,即使是应用 BigDecimal,后果依旧会呈现精度问题。这就波及到创立 BigDecimal 对象时,如果有初始值,是采纳 new BigDecimal 的模式,还是通过 BigDecimal#valueOf 办法了。
之所以会呈现上述景象,是因为 new BigDecimal 时,传入的 0.1 曾经是浮点类型了,鉴于下面说的这个值只是近似值,在应用 new BigDecimal 时就把这个近似值残缺的保留下来了。
而 BigDecimal#valueOf 则不同,它的源码实现如下
public static BigDecimal valueOf(double val) {
// Reminder: a zero double returns '0.0', so we cannot fastpath
// to use the constant ZERO. This might be important enough to
// justify a factory approach, a cache, or a few private
// constants, later.
return new BigDecimal(Double.toString(val));
}在 valueOf 外部,应用 Double#toString 办法,将浮点类型的值转换成了字符串,因而就不存在精度失落问题了。
此时就得出一个根本的论断:第一,在应用 BigDecimal 构造函数时,尽量传递字符串而非浮点类型;第二,如果无奈满足第一条,则可采纳 BigDecimal#valueOf 办法来结构初始化值。
这里延长一下,BigDecimal 常见的构造方法有如下几种:
BigDecimal(int) 创立一个具备参数所指定整数值的对象。BigDecimal(double) 创立一个具备参数所指定双精度值的对象。BigDecimal(long) 创立一个具备参数所指定长整数值的对象。BigDecimal(String) 创立一个具备参数所指定以字符串示意的数值的对象。复制代码
其中波及到参数类型为 double 的构造方法,会呈现上述的问题,应用时需特地注意。
第二:浮点精度的坑
如果比拟两个 BigDecimal 的值是否相等,你会如何比拟?应用 equals 办法还是 compareTo 办法呢?
先来看一个示例:
@Test
public void test2(){BigDecimal a = new BigDecimal("0.01");
BigDecimal b = new BigDecimal("0.010");
System.out.println(a.equals(b));
System.out.println(a.compareTo(b));
}乍一看感觉可能相等,但实际上它们的实质并不相同。
equals 办法是基于 BigDecimal 实现的 equals 办法来进行比拟的,直观印象就是比拟两个对象是否雷同,那么代码是如何实现的呢?
`
@Override
public boolean equals(Object x) {
if (!(x instanceof BigDecimal))
return false;
BigDecimal xDec = (BigDecimal) x;
if (x == this)
return true;
if (scale != xDec.scale)
return false;
long s = this.intCompact;
long xs = xDec.intCompact;
if (s != INFLATED) {
if (xs == INFLATED)
xs = compactValFor(xDec.intVal);
return xs == s;
} else if (xs != INFLATED)
return xs == compactValFor(this.intVal);
return this.inflated().equals(xDec.inflated());
}
仔细阅读代码能够看出,equals 办法不仅比拟了值是否相等,还比拟了精度是否雷同。上述示例中,因为两者的精度不同,所以 equals 办法的后果当然是 false 了。而 compareTo 办法实现了 Comparable 接口,真正比拟的是值的大小,返回的值为 -1(小于),0(等于),1(大于)。根本论断:通常状况,如果比拟两个 BigDecimal 值的大小,采纳其实现的 compareTo 办法;如果严格限度精度的比拟,那么则可思考应用 equals 办法。另外,这种场景在比拟 0 值的时候比拟常见,比方比拟 BigDecimal("0")、BigDecimal("0.0")、BigDecimal("0.00"),此时肯定要应用 compareTo 办法进行比拟。第三:设置精度的坑
在我的项目中看到好多同学通过 BigDecimal 进行计算时不设置计算结果的精度和舍入模式,真是焦急人,尽管大多数状况下不会呈现什么问题。但上面的场景就不肯定了:@Test
public void test3(){
BigDecimal a = new BigDecimal("1.0");
BigDecimal b = new BigDecimal("3.0");
a.divide(b);}
执行上述代码的后果是什么?ArithmeticException 异样!java.lang.ArithmeticException: Non-terminating decimal expansion; no exact representable decimal result.
at java.math.BigDecimal.divide(BigDecimal.java:1690)
...
复制代码
这个异样的产生在官网文档中也有阐明:If the quotient has a nonterminating decimal expansion and the operation is specified to return an exact result, an ArithmeticException is thrown. Otherwise, the exact result of the division is returned, as done for other operations.
总结一下就是,如果在除法(divide)运算过程中,如果商是一个无限小数(0.333…),而操作的后果预期是一个准确的数字,那么将会抛出 ArithmeticException 异样。此时,只需在应用 divide 办法时指定后果的精度即可:@Test
public void test3(){
BigDecimal a = new BigDecimal("1.0");
BigDecimal b = new BigDecimal("3.0");
BigDecimal c = a.divide(b, 2,RoundingMode.HALF_UP);
System.out.println(c);}
复制代码
执行上述代码,输出后果为 0.33。根本论断:在应用 BigDecimal 进行(所有)运算时,肯定要明确指定精度和舍入模式。拓展一下,舍入模式定义在 RoundingMode 枚举类中,共有 8 种:RoundingMode.UP:舍入远离零的舍入模式。在抛弃非零局部之前始终减少数字(始终对非零舍弃局部后面的数字加 1)。留神,此舍入模式始终不会缩小计算值的大小。RoundingMode.DOWN:靠近零的舍入模式。在抛弃某局部之前始终不减少数字(从不对舍弃局部后面的数字加 1,即截短)。留神,此舍入模式始终不会减少计算值的大小。RoundingMode.CEILING:靠近正无穷大的舍入模式。如果 BigDecimal 为正,则舍入行为与 ROUNDUP 雷同; 如果为负,则舍入行为与 ROUNDDOWN 雷同。留神,此舍入模式始终不会缩小计算值。RoundingMode.FLOOR:靠近负无穷大的舍入模式。如果 BigDecimal 为正,则舍入行为与 ROUNDDOWN 雷同; 如果为负,则舍入行为与 ROUNDUP 雷同。留神,此舍入模式始终不会减少计算值。RoundingMode.HALF_UP:向“最靠近的”数字舍入,如果与两个相邻数字的间隔相等,则为向上舍入的舍入模式。如果舍弃局部 >= 0.5,则舍入行为与 ROUND_UP 雷同; 否则舍入行为与 ROUND_DOWN 雷同。留神,这是咱们在小学时学过的舍入模式(四舍五入)。RoundingMode.HALF_DOWN:向“最靠近的”数字舍入,如果与两个相邻数字的间隔相等,则为上舍入的舍入模式。如果舍弃局部 > 0.5,则舍入行为与 ROUND_UP 雷同; 否则舍入行为与 ROUND_DOWN 雷同(五舍六入)。RoundingMode.HALF_EVEN:向“最靠近的”数字舍入,如果与两个相邻数字的间隔相等,则向相邻的偶数舍入。如果舍弃局部右边的数字为奇数,则舍入行为与 ROUNDHALFUP 雷同; 如果为偶数,则舍入行为与 ROUNDHALF_DOWN 雷同。留神,在反复进行一系列计算时,此舍入模式能够将累加谬误减到最小。此舍入模式也称为“银行家舍入法”,次要在美国应用。四舍六入,五分两种状况。如果前一位为奇数,则入位,否则舍去。以下例子为保留小数点 1 位,那么这种舍入形式下的后果。1.15 ==> 1.2 ,1.25 ==> 1.2
RoundingMode.UNNECESSARY:断言申请的操作具备准确的后果,因而不须要舍入。如果对取得准确后果的操作指定此舍入模式,则抛出 ArithmeticException。通常咱们应用的四舍五入即 RoundingMode.HALF_UP。第四:三种字符串输入的坑
当应用 BigDecimal 之后,须要转换成 String 类型,你是如何操作的?间接 toString?先来看看上面的代码:@Test
public void test4(){BigDecimal a = BigDecimal.valueOf(35634535255456719.22345634534124578902);
System.out.println(a.toString());
}
复制代码
执行的后果是上述对应的值吗?并不是:3.563453525545672E+16
复制代码
也就是说,原本想打印字符串的,后果打印进去的是迷信计数法的值。这里咱们须要理解 BigDecimal 转换字符串的三个办法
toPlainString():不应用任何迷信计数法;toString():在必要的时候应用迷信计数法;toEngineeringString():在必要的时候应用工程计数法。相似于迷信计数法,只不过指数的幂都是 3 的倍数,这样不便工程上的利用,因为在很多单位转换的时候都是 10^3;三种办法展现后果示例如下: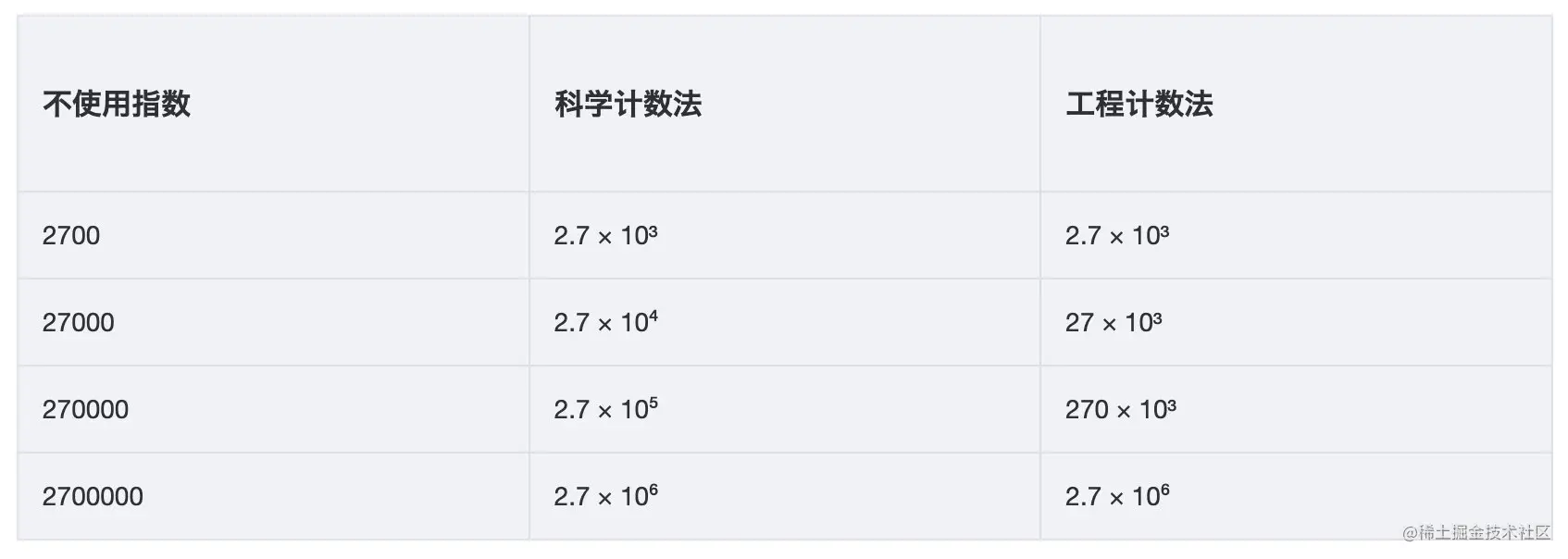
根本论断:依据数据后果展现格局不同,采纳不同的字符串输入办法,通常应用比拟多的办法为 toPlainString()。另外,NumberFormat 类的 format()办法能够应用 BigDecimal 对象作为其参数,能够利用 BigDecimal 对超出 16 位有效数字的货币值,百分值,以及个别数值进行格式化管制。应用示例如下:NumberFormat currency = NumberFormat.getCurrencyInstance(); // 建设货币格式化援用
NumberFormat percent = NumberFormat.getPercentInstance(); // 建设百分比格式化援用
percent.setMaximumFractionDigits(3); // 百分比小数点最多 3 位
BigDecimal loanAmount = new BigDecimal("15000.48"); // 金额
BigDecimal interestRate = new BigDecimal("0.008"); // 利率
BigDecimal interest = loanAmount.multiply(interestRate); // 相乘
System.out.println("金额:\t" + currency.format(loanAmount));
System.out.println("利率:\t" + percent.format(interestRate));
System.out.println("利息:\t" + currency.format(interest));
复制代码
输入后果如下:` 金额: ¥15,000.48
利率: 0.8%
利息: ¥120.00`